Разработка рекомендательной системы на Python.
Думаю, никого сегодня не удивить рекомендательными системами. Их можно встретить повсюду: на сайте с книгами (ozon.ru), блогах (habr.ru), интернет-магазинах (практически любой), стриминговых музыкальных (spotify, Яндекс.Музыка) и видео сервисах (kinopoisk, ivi, amediateka). Самый продуктивный способ разобраться как работают подобные алгоритмы — написать самому с самого начала. Этому и будет посвящена текущая статья.
В рекомендательных системах есть два основных подхода:
- Content-based рекомендации основанные на описании объектов, которые требуется рекомендовать (рекомендуем фильмы, похожие на те, которые понравились пользователю);
- Коллаборативная фильтрация основанная на оценках пользователя и похожести его на других пользователей.
Первый подход более трудоёмкий и сильно привязан к конкретной предметной области. Второй — значительно проще, но имеет недостатки. Например, проблема “холодного старта”: что рекомендовать новым пользователям, которые не оценили ни одного фильма или кому рекомендовать фильм, у которого ещё не оценок?
В этой статье определим рекомендации на основе коллаборативной фильтрации.
На просторах интернета мне удалось найти набор данных с оценками пользователей различным фильмам. Набор данных оказался довольно объемным:
import numpy as np
import pandas as pd
ratings_df = pd.read_csv('./ml-20m/ratings.csv')
print('Unique users count: {}'.format(len(ratings_df['userId'].unique())))
print('Unique movies count: {}'.format(len(ratings_df['movieId'].unique())))
print('DataFrame shape: {}'.format(ratings_df.shape))
ratings_df.head()
# Unique users count: 671
# Unique movies count: 9066
# DataFrame shape: (100004, 4)
| userId | movieId | rating | timestamp | |
|---|---|---|---|---|
| 0 | 1 | 31 | 2.5 | 1260759144 |
| 1 | 1 | 1029 | 3.0 | 1260759179 |
| 2 | 1 | 1061 | 3.0 | 1260759182 |
| 3 | 1 | 1129 | 2.0 | 1260759185 |
| 4 | 1 | 1172 | 4.0 | 1260759205 |
Для нашего “эксперимента на кошечках” достаточно будет первых 100000 записей всего набора:
n = 100000
ratings_df_sample = ratings_df[:n]
n_users = len(ratings_df_sample['userId'].unique())
n_movies = len(ratings_df_sample['movieId'].unique())
(n_users, n_movies)
# (671, 9066)
Итого в выборку попало 671 пользователь и 9066 фильмов.
Для дальнейшего удобства отмасштабируем идентификаторы фильмов таким образом, чтобы они начинались с 1 и заканчивались на n_movies:
movie_ids = ratings_df_sample['movieId'].unique()
def scale_movie_id(movie_id):
scaled = np.where(movie_ids == movie_id)[0][0] + 1
return scaled
ratings_df_sample['movieId'] = ratings_df_sample['movieId'].apply(scale_movie_id)
ratings_df_sample.head()
| userId | movieId | rating | timestamp | |
|---|---|---|---|---|
| 0 | 1 | 1 | 2.5 | 1260759144 |
| 1 | 1 | 2 | 3.0 | 1260759179 |
| 2 | 1 | 3 | 3.0 | 1260759182 |
| 3 | 1 | 4 | 2.0 | 1260759185 |
| 4 | 1 | 5 | 4.0 | 1260759205 |
Разделим весь набор данных на две части: обучающий и тестовый. Из названия должно быть понятно, что первый будет использоваться для обучения, а на втором будет измеряться качество предсказанных оценок. Разделить набор можно при помощи фукции train_test_split из модуля scikit-learn:
from sklearn import cross_validation as cv
train_data, test_data = cv.train_test_split(ratings_df_sample, test_size=0.2)
print('Train shape: {}'.format(train_data.shape))
print('Test shape: {}'.format(test_data.shape))
# Train shape: (80000, 4)
# Test shape: (20000, 4)
Для определения качества предсказанных оценок воспользуемся мерой RMSE (Root Mean Square Error, среднеквадратическая ошибка):
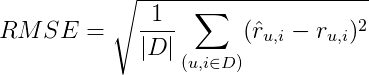
Среднеквадратическая ошибка представляет собой корень из средней ошибки по всем оценкам, данным нашим алгоритмом. Проще показать на примере.
Допустим, у нас имеется следующий набор оценок:
| user | movie | rating | predicted |
|---|---|---|---|
| Anna | Thor 1 | 5 | 3 |
| Anna | Thor 2 | 5 | 5 |
| Anna | Thor 3 | 5 | 1 |
| Vova | Thor 1 | 4 | 4 |
| Vova | Thor 2 | 1 | 3 |
| Vova | Ant-man | 5 | 3 |
| Vova | Hulk | 3 | 1 |
| Inna | Thor 1 | 1 | 5 |
| Inna | Ant-man | 5 | 5 |
| Ivan | Thor 1 | 5 | 5 |
| Ivan | Thor 3 | 5 | 5 |
| Ivan | Hulk | 5 | 1 |
Колонка predicted содержит предсказанные алгоритмом оценки (на самом деле тоже случайные, как и оценки в колонке rating). В этом случае мера RMSE будет следующей:
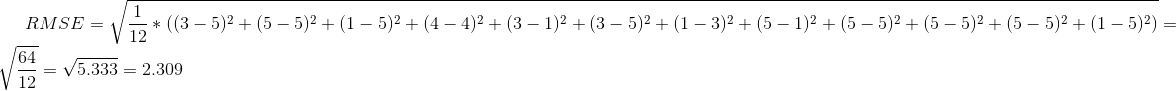
from sklearn.metrics import mean_squared_error
from math import sqrt
def rmse(prediction, ground_truth):
# Оставим оценки, предсказанные алгоритмом, только для соотвествующего набора данных
prediction = np.nan_to_num(prediction)[ground_truth.nonzero()].flatten()
# Оставим оценки, которые реально поставил пользователь, только для соотвествующего набора данных
ground_truth = np.nan_to_num(ground_truth)[ground_truth.nonzero()].flatten()
mse = mean_squared_error(prediction, ground_truth)
return sqrt(mse)
Сформируем матрицы размера (n_users, n_movies) для обучающего и тестового наборов таким образом, чтобы элемент в ячейке [i, j] отражал оценку i-го пользователя j-му фильму:
train_data_matrix = np.zeros((n_users, n_movies))
for line in train_data.itertuples():
train_data_matrix[line[1] - 1, line[2] - 1] = line[3]
test_data_matrix = np.zeros((n_users, n_movies))
for line in test_data.itertuples():
test_data_matrix[line[1] - 1, line[2] - 1] = line[3]
Ещё раз отмечу, что часть оценок попала в обучающий набор train_data_matrix, а другая часть — test_data_matrix для того, чтобы можно было измерить качество предсказаний.
Один из важных моментов в коллаборативной фильтрации — найти похожих пользователей для User-Based и похожие объекты (в нашем случае фильмы) для Item-Based коллаборативной фильтрации. Для этого существуют различные подходы. Один из них — использовать косинусное расстояние между векторами, описывающими пользователей и объекты. В модуле scikit-learn существует готовая функция:
from sklearn.metrics.pairwise import pairwise_distances
# считаем косинусное расстояние для пользователей и фильмов
# (построчно и поколоночно соотвественно).
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')
То есть user_similarity[i][j] — косинусное расстояние между i-ой строкой и j-ой строкой (можно проверить через scipy.spatial.distance.cosine(x,y)), а item_similarity[i][j] — косинусное расстояние между i-ой и j-ой колонками.
Можно считать, что косинусное расстояние обозначает степень похожести. Чем пользователи или фильмы более похожи друг на друга — тем меньше будет косинусное расстояние:
from scipy.spatial import distance
print(distance.cosine([2,2],[1,1]))
print(distance.cosine([3,3],[2,3]))
print(distance.cosine([3, 3],[1, 1.5]))
print(distance.cosine([3, 3],[1, 3]))
# 2.2204460492503131e-16
# 0.019419324309079666
# 0.019419324309079666
# 0.10557280900008403
В последующих примерах будет два метода: один для User-base коллаборативной фильтрации (основанной на похожести пользователей) и второй для Item-Based коллаборативной фильтрации (основанной на похожести фильмов). По сути — это один и тот же алгоритм, но во втором случае используется транспонированная матрица оценок (фильмы располагаются в строках, а пользователи — в колонках).
Наивные рекомендации
Самая простейшая рекомендательная система считает предсказанную оценку пользователя u фильму i по формуле:
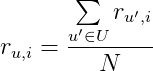
где
N— количество пользователей, похожих на пользователяu,U— множество изNпохожих пользователей,u'— пользователь, похожий на пользователяu(из множестваU),r_{u', i}— оценка пользователяu'фильмуi,r_{u,i}— предсказанная оценка фильмаi.
По этой формуле предсказываемая оценка фильму i пользователя u равняется средней оценке фильма i от N пользователей, наиболее похожих на пользователя u.
Рассмотрим небольшой пример (будем возвращаться к нему и далее). У нас имеется набор оценок пользователей следующего вида:
| user | movie | rating |
|---|---|---|
| Anna | Thor 1 | 5 |
| Anna | Thor 2 | 5 |
| Anna | Thor 3 | 5 |
| Vova | Thor 1 | 4 |
| Vova | Thor 2 | 1 |
| Vova | Ant-man | 5 |
| Vova | Hulk | 3 |
| Inna | Thor 1 | 1 |
| Inna | Ant-man | 5 |
| Ivan | Thor 1 | 5 |
| Ivan | Thor 3 | 5 |
| Ivan | Hulk | 5 |
Для более удобной работу таблицу стоит привести к другому виду:
| Thor 1 | Thor 2 | Thor 3 | Ant-man | Hulk | |
|---|---|---|---|---|---|
| Anna | 5 | 5 | 5 | 0 | 0 |
| Vova | 4 | 1 | 0 | 5 | 3 |
| Inna | 1 | 0 | 0 | 5 | 0 |
| Ivan | 5 | 0 | 5 | 0 | 4 |
Как говорили выше, для меры близости будем использовать косинусное расстояние:
from sklearn.metrics.pairwise import pairwise_distances
demo_data = [[5,5,5,0,0], [4,1,0,5,3], [1,0,0,5,0], [5,0,5,0,4]]
pairwise_distances(demo_data, metric='cosine')
# array([[ 0. , 0.59577396, 0.8867723 , 0.28933095],
# [ 0.59577396, 0. , 0.2036092 , 0.4484398 ],
# [ 0.8867723 , 0.2036092 , 0. , 0.87929886],
# [ 0.28933095, 0.4484398 , 0.87929886, 0. ]])
Для удобства перепишем матрицу таким образом, чтобы в строках и колонках были имена пользователей:
| Anna | Vova | Inna | Ivan | |
|---|---|---|---|---|
| Anna | 0 | 0.5957 | 0.8867 | 0.2893 |
| Vova | 0.5957 | 0 | 0.2036 | 0.4484 |
| Inna | 0.8867 | 0.2036 | 0 | 0.8792 |
| Ivan | 0.2893 | 0.4484 | 0.8792 | 0 |
В полученной матрице число в ячейке [i, j] отражает похожесть пользователя i и j. В нашем примере число 0.59577396 в ячейке [0, 1] — косинусное расстояние между оценками Анны и Вовы.
Допустим, что N равно двум. Двумя наиболее похожими на Анну пользователями будут Иван (расстояние равно 0.2893) и Вова (расстояние равно 0.5957); для Вовы — Инна и Иван (расстояния 0.2036 и 0.4484 соответственно); для Инны — Вова и Иван (расстояние 0.2036 и 0.8792 соответственно); для Ивана — Анна и Вова (расстояние 0.2893 и 0.4484 соответственно).
Следуя формуле в начале раздела посчитаем ожидаемую оценку Анны для фильмов Ant-man и Hulk.
Для Ant-man:
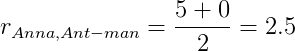
Для Hulk:
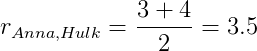
# User-based collaborative filtering
def naive_predict(top):
# Структура для хранения для каждого пользователя оценки фильмов top наиболее похожих на него пользователей:
# top_similar_ratings[0][1] - оценки всех фильмов одного из наиболее похожих пользователей на пользователя с ид 0.
# Здесь 1 - это не ид пользователя, а просто порядковый номер.
top_similar_ratings = np.zeros((n_users, top, n_movies))
for i in range(n_users):
# Для каждого пользователя необходимо получить наиболее похожих пользователей:
# Нулевой элемент не подходит, т.к. на этом месте находится похожесть пользователя самого на себя
top_sim_users = user_similarity[i].argsort()[1:top + 1]
# берём только оценки из "обучающей" выборки
top_similar_ratings[i] = train_data_matrix[top_sim_users]
pred = np.zeros((n_users, n_movies))
for i in range(n_users):
pred[i] = top_similar_ratings[i].sum(axis=0) / top
return pred
def naive_predict_item(top):
top_similar_ratings = np.zeros((n_movies, top, n_users))
for i in range(n_movies):
top_sim_movies = item_similarity[i].argsort()[1:top + 1]
top_similar_ratings[i] = train_data_matrix.T[top_sim_movies]
pred = np.zeros((n_movies, n_users))
for i in range(n_movies):
pred[i] = top_similar_ratings[i].sum(axis=0) / top
return pred.T
naive_pred = naive_predict(7)
print('User-based CF RMSE: ', rmse(naive_pred, test_data_matrix))
naive_pred_item = naive_predict_item(7)
print('Item-based CF RMSE: ', rmse(naive_pred_item, test_data_matrix))
# User-based CF RMSE: 2.81961691384066
# Item-based CF RMSE: 3.001291898703705
Рекомендации с учётом средних оценок похожих пользователей
Менее наивная реализация требует участия матрицы “похожести” и оценок “похожих” пользователей. Формула вычисления предсказанной оценки:
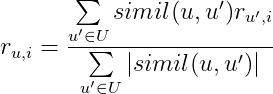
где
simil(u, u')— “похожесть” пользователяuи пользователяu',r_{u', i}— оценка пользователя u’ из U фильму i,U,u'— аналогичны предыдущей формуле.
То есть предсказываемая оценка фильму будет равна сумме произведений “похожести” пользователя на его оценку по всем наиболее похожим пользователям.
Посчитаем предсказанные оценки Анны для Ant-man и Hulk по этой формуле.
Для Ant-man:
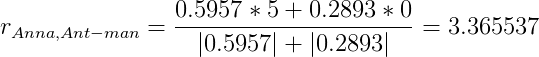
Для Hulk:
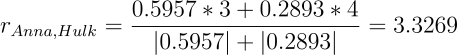
def k_fract_predict(top):
top_similar = np.zeros((n_users, top))
for i in range(n_users):
user_sim = user_similarity[i]
top_sim_users = user_sim.argsort()[1:top + 1]#[-top:]
for j in range(top):
top_similar[i, j] = top_sim_users[j]
abs_sim = np.abs(user_similarity)
pred = np.zeros((n_users, n_movies))
for i in range(n_users):
indexes = top_similar[i].astype(np.int)
numerator = user_similarity[i][indexes]
product = numerator.dot(train_data_matrix[indexes])
denominator = abs_sim[i][top_similar[i].astype(np.int)].sum()
pred[i] = product / denominator
return pred
def k_fract_predict_item(top):
flag = True
top_similar = np.zeros((n_movies, top))
for i in range(n_movies):
movies_sim = item_similarity[i]
top_sim_movies = movies_sim.argsort()[1:top + 1]
for j in range(top):
top_similar[i, j] = top_sim_movies.T[j]
abs_sim = np.abs(item_similarity)
pred = np.zeros((n_movies, n_users))
for i in range(n_users):
indexes = top_similar[i].astype(np.int)
numerator = item_similarity[i][indexes]
product = numerator.dot(train_data_matrix.T[indexes])
denominator = abs_sim[i][indexes].sum()
denominator = denominator if denominator != 0 else 1
pred[i] = product / denominator
return pred.T
k_predict = k_fract_predict(7)
print('User-based CF RMSE: ', rmse(k_predict, test_data_matrix))
k_predict_item = k_fract_predict_item(7)
print('Item-based CF RMSE: ', rmse(k_predict_item, test_data_matrix))
# User-based CF RMSE: 2.821055763616836
# Item-based CF RMSE: 3.245023071118644
Жаль, но на тех же входных данных результат получился несколько хуже, чем при наивной реализации.
Рекомендации на основе средних оценок пользователей и матрицы “похожести”
Третья реализация зависит от оценок, которые пользователь ставил ранее (точнее, от средней оценки по всем оценённым пользователем фильмам), средних оценок “похожих” пользователей и коэффициентов “похожести”:
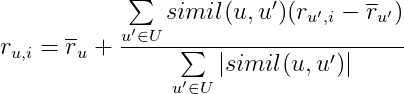 ,
,
где r с чертой — средняя оценка соответствующего пользователя, а остальные переменные формулы уже обсуждались выше.
Воспользуемся этой формулой для предсказания оценок Анны фильмам Ant-man и Hulk. Для этого потребуются средние рейтинги по всем оценённым фильмам для Анны, Ивана и Вовы. Они равны 5, 4.666667, 3.25 соответственно.
Оценка для фильма Ant-man:
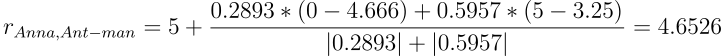
Оценка для фильма Hulk:
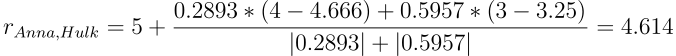
Если вы нашли ошибку в вычислениях — пишите в комментариях и я исправлю при первой же возможности.
def k_fract_mean_predict(top):
top_similar = np.zeros((n_users, top))
for i in range(n_users):
user_sim = user_similarity[i]
top_sim_users = user_sim.argsort()[1:top + 1]
for j in range(top):
top_similar[i, j] = top_sim_users[j]
abs_sim = np.abs(user_similarity)
pred = np.zeros((n_users, n_movies))
for i in range(n_users):
indexes = top_similar[i].astype(np.int)
numerator = user_similarity[i][indexes]
mean_rating = np.array([x for x in train_data_matrix[i] if x > 0]).mean()
diff_ratings = train_data_matrix[indexes] - train_data_matrix[indexes].mean()
numerator = numerator.dot(diff_ratings)
denominator = abs_sim[i][top_similar[i].astype(np.int)].sum()
pred[i] = mean_rating + numerator / denominator
return pred
def k_fract_mean_predict_item(top):
top_similar = np.zeros((n_movies, top))
for i in range(n_movies):
movie_sim = item_similarity[i]
top_sim_movies = movie_sim.argsort()[1:top + 1]
for j in range(top):
top_similar[i, j] = top_sim_movies[j]
abs_sim = np.abs(item_similarity)
pred = np.zeros((n_movies, n_users))
for i in range(n_movies):
indexes = top_similar[i].astype(np.int)
numerator = item_similarity[i][indexes]
diff_ratings = train_data_matrix.T[indexes] - train_data_matrix.T[indexes].mean()
numerator = numerator.dot(diff_ratings)
denominator = abs_sim[i][top_similar[i].astype(np.int)].sum()
denominator = denominator if denominator != 0 else 1
mean_rating = np.array([x for x in train_data_matrix.T[i] if x > 0]).mean()
mean_rating = 0 if np.isnan(mean_rating) else mean_rating
pred[i] = mean_rating + numerator / denominator
return pred.T
k_predict = k_fract_mean_predict(7)
print('User-based CF RMSE: ', rmse(k_predict, test_data_matrix))
k_predict_item = k_fract_mean_predict_item(7)
print('Item-based CF RMSE: ', rmse(k_predict_item, test_data_matrix))
# User-based CF RMSE: 1.5491818781971805
# Item-based CS RMSE: 1.283294405965073
В этом варианте получили лучший результат для User-based коллаборативной фильтрации. Для Item-based лучшей осталась наивная реализация.
Заключение
Сводка полученных результатов в качестве подведения итогов:
| Method 1 | Method 2 | Method 3 | |
|---|---|---|---|
| User-Based | 2.819 | 2.821 | 1.549 |
| Item-Based | 3.001 | 3.245 | 1.283 |
Таким образом, лучшим на наших данных оказался третий подход.
Как оказалось, простую рекомендательную систему сделать несложно: достаточно совсем немного математики. При этом результаты получаются приемлемые.
Полученные этими алгоритмами рекомендации не сравнятся с рекомендациями специализированных сервисов. Например, таких как Netflix или Spotify, но и ресурсов эти подходы требуют значительно меньше.
Серьёзные компании, такие как Spotify, например, подходят к рекомендациям гораздо основательнее.
В следующей статье вернёмся к теме рекомендательных систем и сделаем Content-Based рекомендательную систему, учитывающую больше признаков.
Ссылки
- [RU] recommender-systems-in-python (GihHub)
- [RU] Как работают рекомендательные системы. Лекция в Яндексе (Habrahabr)
- [EN] Collaborative filtering (Wikipedia)
P.S. Вполне вероятно, в коде или вычислениях есть ошибки. Буду признателен, если вы укажете на них в комментариях.
